| First Steps in Programming RISC OS Computers |
|
| Martyn Fox |
Chapter 9 : Bits, Bytes and Binary numbers
Be warned! This section may seem a bit tedious at first but, if you stick with it, you'll understand more about your computer and the workings of ASCII codes and colour numbers.
Our counting system is based on the number ten. We use single-digit numbers up to 9, then put a '1' on the left and set the units back to zero. When the count reaches 99, we add another digit. The number '100' means 'ten times ten', '1000' means 'ten times ten times ten' and so on. We say that ten is the base of our numbers and we call them decimal numbers.
There is no mathematical reason why we have to use a base of ten, except that everybody does it and we all understand it. It's commonly supposed that early man learnt to count on his fingers and thumbs and, of course, we have ten of those!
Changing the Base
A better system might have been based on twelve, because it's divisible by two, three, four and six while ten is only divisible by two and five. In this case, '10' would mean the number we think of as twelve and we would have to invent two extra squiggles to represent ten and eleven.How does a computer store and process numbers? If it worked with a base of ten as we do, each element in its memory would have to be capable of being set in ten different states to remember one digit. If we represented a number by a voltage on a wire, we would have to use ten different voltages. The voltage representing 'five' would not be very different from the voltages for four and six and it could very easily make a mistake.
It would be a lot easier to design the machine if it used numbers with a base less than ten - the smaller the better. What is the smallest base it is possible to have for a counting system? Two!
Binary Numbers
Numbers with a base of two have only two digits - 0 and 1 - and are known as binary numbers. They can be handled very easily by a computer and all computers, including your RISC OS machine, use them. Each element of your computer's memory can be set in one of two states, rather like a switch that can be on or off.Let's see what binary numbers look like:
| Decimal | Binary | |
| 0 | 0 | |
| 1 | 1 | |
| 2 | 10 | |
| 3 | 11 | |
| 4 | 100 | |
| 5 | 101 | |
| 6 | 110 | |
| 7 | 111 | |
| 8 | 1000 | |
| 9 | 1001 | |
| 10 | 1010 | |
| 11 | 1011 | |
| 12 | 1100 | |
| 13 | 1101 | |
| 14 | 1110 | |
| 15 | 1111 | |
| 16 | 10000 | |
If you examine the numbers in the right-hand column you'll see a definite pattern. Where a number consists of a '1' followed by several noughts, the number in the left-hand column is always a power of 2, that is 2 multiplied by itself a certain number of times. This is to be expected, as all decimal numbers which consist of a '1' plus several noughts are powers of ten, for example 100, 1000, 10,000 etc.
This also means that a number which is all '1's is always one less than a power of 2, for example 3, 7 and 15. These are also the highest numbers that can be represented by a given number of binary digits.
Bits and Bytes
In computing, each 0 or 1 is called a bit, which you can think of as being short for binary digit. You may have noticed that your machine is referred to as a 32-bit computer. This means that its ARM processor can handle a number consisting of 32 bits at the same time. They move round the machine on 32 wires, known as the data bus (they are actually tracks on the printed circuit board). A older 16-bit machine had a data bus consisting of 16 wires, and older machines still, such as the BBC Model B and Master, used 8 bits.We refer to 8 bits as a byte. The highest number that a byte can hold is 11111111, which in decimal is 255. Does that number seem familiar? It's one less than the highest number of colours we can have on the screen at any one time in certain modes, it's the highest number we can use when defining colours and it's also the highest number that we can use for ASCII codes (though we usually only use codes up to 127, which in binary is 01111111).
There are no prizes for guessing that each of these things is represented by one byte. Numbers which are powers of two (or 1 less than them) keep cropping up in computing, so it's handy to be familiar with them. Let's list some of them:
| Decimal | Binary | ||
| 21 | 2 | 10 | |
| 22 | 4 | 100 | |
| 23 | 8 | 1000 | |
| 24 | 16 | 10000 | |
| 25 | 32 | 100000 | |
| 26 | 64 | 1000000 | |
| 27 | 128 | 10000000 | |
| 28 | 256 | 100000000 | |
You can see one of the snags with binary numbers - they are very long! We've only got up to 256 and already the number has nine digits. A number such as 14,146 in binary would be:
11 0111 0100 0010
This is a bit of a handful, and it's by no means the largest number your machine will handle. We need a shorthand way of referring to binary numbers, one which will allow us to see where all the '1's and '0's are.
What the Hexadecimal?
The clue to doing this lies in the way we just displayed the number. You may have noticed that the digits are grouped in fours, with spaces between them. Suppose we take each group and represent it by the decimal number that it makes up:11 0111 0100 0010 3 7 4 2
Each of these groups of four bits can represent a number up to 15. You can perhaps see that grouping them in this way is the equivalent of inventing a numbering system with a base of 16, and that is precisely what we've done. The number at the bottom is, in fact:
3 x 16 x 16 x 16
+ 7 x 16 x 16
+ 4 x 16
+ 2
which happens to add up to 14,146, the number represented by the binary number that we started with.
Numbers with a base of 16 are known as hexadecimal numbers, and can actually have fewer digits than their decimal equivalents. We usually write them with an ampersand or '&' sign in front, to show they are hexadecimal. Thus &3742 is the hexadecimal version of 14,146.
So far so good. Suppose, though, the number we wanted to represent was, say, 14,155. In binary, with the equivalent numbers underneath, this would be:
11 0111 0100 1011 3 7 4 11
Now you can see we have a problem. The right-hand group of four bits make a number greater than nine, so we need a two-digit decimal number to represent them. We could hardly write down the hexadecimal version of 14,155 as &37411, as this wouldn't convey the fact that the last two digits stand for one group of four bits.
At the beginning of the section we saw how we could use a counting system with a base of twelve, provided we invented a couple of extra squiggles to represent ten and eleven. Because hexadecimal numbers have a base of 16, we need six extra squiggles, to represent numbers 10 to 15. By convention, we use capital letters A to F, so that the full set of hexadecimal characters up to 15 looks like this:
| Decimal | Hexadecimal | Binary |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 10 |
| 3 | 3 | 11 |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
So the hexadecimal equivalent of 14,155 becomes &374B.
You can show this by entering Basic and typing:
PRINT &374B
Basic knows that the number you want it to print is hexadecimal because you precede it with an '&' symbol, so you should get the answer 14155. To go the other way and tell it to print a number in hexadecimal form, we use the tilde or '~' character, so that:
PRINT ~14155
will give you the answer 374B.
Negative Binary Numbers
Hexadecimal numbers are particularly useful when dealing with the 32-bit numbers that your machine is capable of handling. The largest number that can be represented by 32 bits is 32 '1's, which in binary looks like this:1111 1111 1111 1111 1111 1111 1111 1111
This would be written in hexadecimal form as &FFFFFFFF which is a lot shorter!
In fact, by convention, any number whose left-most bit is a '1' is usually taken to be a negative number. This is the case if the left-hand hexadecimal digit is 8 or higher.
The number &FFFFFFFF is actually 1. To understand this, think of a mechanical counter like a car mileometer, counting downwards. When the figures pass through zero, they go to a row of nines. Thus, if the counter has four digits, you can think of 9999 as 1, 9998 as 2 and so on.
It's the same with binary and hexadecimal numbers. &FFFFFFFF (all '1's) represents 1, &FFFFFFFE (all '1's except the right-hand bit) is 2 and so on.
You can see this for yourself by entering Basic and typing:
PRINT &FFFFFFFF
This explains why the value of TRUE is 1. FALSE is a number which is all zeros; TRUE is a number which is all ones.
The largest positive and negative numbers that you can represent using 32-bit hexadecimal numbers are &7FFFFFFF and &80000000, which are 2147483647 and 2147483648 respectively. These also happen to be the largest values of integer variables - this is because an integer variable is held in 32 bits or four bytes.
By the way, half a byte, or four bits, is occasionally referred to as a nibble, or nybble if you like. Four bytes, or 32 bits, are not known as a gobble though, but as a word. Your RISC OS machine does a lot of work with words because it handles 32 bits at a time.
ASCII Codes Explained
Now let's take another look at ASCII codes which we first encountered in Section 8. You may have wondered why the codes for numbers started at 48, capital letters at 65 and lower case letters at 97. There was a clue in the fact that the codes were listed in columns of 32 characters.We've listed the codes again on the opposite page, this time in hexadecimal form. To remind you, &20 is a space and &7F is backspace and delete.
You can now see that, in hexadecimal form, ASCII codes for numbers start at &30.
If we look at the bit pattern for, say, &36, it looks like this:
0011 0110 3 6
If we could turn all the 1s in the left half of the number to zeros, we would be left with the binary number 6 which is, of course, the digit which the ASCII code represents.
| 20 | space | 40 | @ | 60 | ` |
| 21 | ! | 41 | A | 61 | a |
| 22 | " | 42 | B | 62 | b |
| 23 | # | 43 | C | 63 | c |
| 24 | $ | 44 | D | 64 | d |
| 25 | % | 45 | E | 65 | e |
| 26 | & | 46 | F | 66 | f |
| 27 | ' | 47 | G | 67 | g |
| 28 | ( | 48 | H | 68 | h |
| 29 | ) | 49 | I | 69 | i |
| 2A | * | 4A | J | 6A | j |
| 2B | + | 4B | K | 6B | k |
| 2C | , | 4C | L | 6C | l |
| 2D | - | 4D | M | 6D | m |
| 2E | . | 4E | N | 6E | n |
| 2F | / | 4F | O | 6F | o |
| 30 | 0 | 50 | p | 70 | P |
| 31 | 1 | 51 | Q | 71 | q |
| 32 | 2 | 52 | R | 72 | r |
| 33 | 3 | 53 | S | 73 | s |
| 34 | 4 | 54 | T | 74 | t |
| 35 | 5 | 55 | U | 75 | u |
| 36 | 6 | 56 | V | 76 | v |
| 37 | 7 | 57 | W | 77 | w |
| 38 | 8 | 58 | X | 78 | x |
| 39 | 9 | 59 | Y | 79 | y |
| 3A | : | 5A | Z | 7A | z |
| 3B | ; | 5B | [ | 7B | { |
| 3C | < | 5C | \ | 7C | | |
| 3D | = | 5D | ] | 7D | } |
| 3E | > | 5E | ^ | 7E | ~ |
| 3F | ? | 5F | _ | 7F | delete |
Letter Codes Investigated
Now let's look at the codes for an upper case and lower case letter, using G and g as our example:0100 0111 4 7 0110 0111 6 7
The only difference between the codes is that the sixth bit from the right (usually referred to as bit 5) is 0 for upper case and 1 for lower case. This applies to any letter of the alphabet. It may also be worth noting that the number in the five right-hand bits is the position in the alphabet of the letter; 7 in the case of G.
If we could change the state of bit 5 (that is from 0 to 1 or 1 to 0), we could turn a letter from upper case to lower case or vice versa. This could be useful, particularly if we wanted to check to see if we had typed in a particular string. Suppose, for example, you wanted to find out whether or not the user's name is Fred. You could use this program, called Fred:
10 REM > Fred 20 REM Checks to see if 'Fred' typed 30 ON ERROR REPORT:PRINT " at line ";ERL:END 40 INPUT "What is your name? "name$ 50 IF name$="Fred" PRINT "That's right" ELSE PRINT "That's wrong"
If you type in 'Fred', the program will answer 'That's right', and if you type something else, it will answer 'That's wrong'. Unfortunately, it will also say 'That's wrong' if you type 'FRED' or 'fred', which may not be what you wanted it to do.
We could get round this problem if we had some way of converting any lower case characters that we enter to capitals and then comparing the string with 'FRED'. For this we need some way of manipulating the bits.
Boolean Algebra
A 19th century mathematician named George Boole invented a form of algebra in which all the variables have the value 1 or 0. These variables could be combined together in two ways, known as AND and OR.The rules are as follows:
- x AND y AND z = 1 only if x, y and z are all 1. If any of them is 0, the result is 0.
- x OR y OR z = 1 if any of x, y and z is 1. The result is only 0 if they are all 0.
We can also invert a variable by using NOT so that, if x is 1, NOT x is 0 and vice versa.
This form of algebra became known as Boolean Algebra. It's difficult to see what possible use it could have been in the 19th century, but it now forms the basis of all computers, because it's a very convenient way of manipulating binary numbers!
Modern computers and other digital equipment contain a great many logic gates. These are simple electronic circuits which mimic AND and OR functions and which are known as AND gates and OR gates. A logic gate responds to voltages on its input pins which correspond to 1 or 0 to produce a similar voltage on its output pin.
Logic Operations on Bits
You can also do AND and OR operations on numbers in Basic. Each bit of one number is ANDed or ORed with the corresponding bit of another number to produce the result. To show this, enter Basic and type:PRINT 6 AND 3
You should get the answer 2.
To understand this, look at 6 and 3 in binary (we need only concern ourselves with the lowest bits in this case):
| 6 | 0110 |
| 3 | 0011 |
| 6 AND 3 | 0010 |
Each digit in the bottom row is the result of doing an AND operation on the two digits above it. To remind you, the result is only 1 if both the top two digits are 1. This only applies in one column (bit 1, the second from the right), so the result is 0010, which is 2.
Now try another example:
PRINT 6 OR 3
This time the answer is 7. In binary, it works like this:
| 6 | 0110 |
| 3 | 0011 |
| 6 OR 3 | 0111 |
We get a 1 on the bottom line wherever there is a 1 in either of the lines above.
It's clearly much easier to use hexadecimal numbers for this than decimal ones as you can work out the states of the individual bits.
Now try typing:
PRINT NOT 0
and
PRINT NOT 1
What's NOT Zero?
You may be surprised to find that NOT 0 is 1 and even more surprised that NOT 1 is 2, until you remember that, in hexadecimal, 1 is written as &FFFFFFFF and 2 as &FFFFFFFE.The NOT operation has been applied to all 32 bits of the number. In the case of 0, they've all been turned from 0 to 1, producing &FFFFFFFF or 1. In the case of 1, they've all been turned from 0 to 1 except for bit 0, which is already 1, and so is turned from 1 to 0. This produces &FFFFFFFE or 2.
These AND, OR and NOT operations are known as logic operations. There is one more, known as exclusive or, or EOR, which can be applied to two numbers. The rule here is that, if the bits are different (one is 1 and the other is 0), the result is a 1, and if they are the same, either both 0 or both 1, the result is 0.
It is possible to manipulate the individual bits of a number by doing a logic operation on it, together with a mask number, whose bits are in whatever state you need to do the operation.
- To force a bit to 1, set the corresponding bit in the mask to 1 and do an OR operation. The other bits in the mask should all be zeros.
- To force a bit to 0, set the corresponding bit in the mask to 0 and do an AND operation. The other bits in the mask should all be ones.
- To invert a bit, set the corresponding bit in the mask to 1 and do an EOR operation. The other bits in the mask should all be zeros.
We can use these techniques to get a number from its ASCII code in a program called Ascnum:
10 REM > Ascnum 20 REM derives a number from its ASCII code 30 ON ERROR REPORT:PRINT " at line ";ERL:END 40 PRINT "Enter a number (0 - 9)" 50 code%=GET 60 num%=code% AND &F 70 PRINT "Twice that number is ";num%*2
Line 50 sets the variable code% to the ASCII code of the key you press. If the number is, say, 5, code% will be &35, or 0011 0101. To convert this code to the number it represents, we have to force the left-hand set of four bits to zero, leaving 0000 0101 to represent 5. We do this in line 60 by ANDing code% with &F, which is 0000 1111. This is our mask number. Because the four right-hand bits of this number are 1, the right-hand bits of &35 are left alone. All the bits of the mask number apart from these four are zero, which has the effect of forcing the corresponding bits of code% to zero. This turns 0011 0101 into 0000 0101, which is 5.
Changing Case of Letters
This is the technique we need to convert all the characters of a string to upper case in our Fred program. All upper case letters have an ASCII code &4x or &5x, where x is any hexadecimal character (this also applies to the six characters with codes &5A to &5F, but this needn't bother us). Similarly, all lower case letters have codes &6x or &7x.In binary, this appears as follows:
Upper case: 010x xxxx
Lower case: 011x xxxx
where x can be 0 or 1. This covers all letters of the alphabet.
You can see that converting lower case to upper case is done by forcing bit 5 to 0. As we saw earlier, we can do this with an AND operation. We must leave all the other bits alone, so we need a mask number which has a zero in bit 5 and ones in all the other bits, in other words 1101 1111. In hexadecimal form this is &DF.
If we wanted to convert a letter to lower case, we would have to force bit 5 to 1. We would do this with an OR operation, using 0010 0000 as a mask number, or &20.
We can use both these techniques in a new version of our Fred program, called Fred2:
You can type in a name using any combination of upper and lower case letters, and the program will repeat it back to you with a capital for the first letter and the rest in lower case.
ASC and CHR$
In this program, we're using two new Basic keywords, ASC and CHR$. ASC produces the ASCII code for the first character of the string which follows it and CHR$ does the opposite, producing a string containing one character whose ASCII code is the number following it. Try typing:PRINT ASC"A"
You should get 65 which, you will remember, is the ASCII code for 'A'. Now try:
PRINT CHR$65
You should get 'A'.
Line 50 gets the ASCII code for the first character of name$ and puts it into variable char%. This is the character that we wish to convert to upper case, so we AND it with &DF in line 60. In line 70 we begin to create a new string, name2$, giving it a character whose ASCII code is the new value of char%. This is the same letter as the first character of name$, but converted to upper case if necessary.
We don't actually need the brackets and the LEFT$ arrangement in line 50, as the ASC keyword will give us the code for the first character of the string anyway, but their presence makes the meaning of the line a little clearer.
In line 80, we start a FOR ... NEXT loop. We use this to select each letter of name$ in turn, beginning with the second one and continuing until we reach the end of the string, when n%=LENname$. We make char% the ASCII code of the character in the same way as before, but using MID$ this time to produce a one-character string containing the letter that we're dealing with. Line 100 converts this character to lower case and line 110 adds the result to our new string. You may remember that this is a short way of writing:
name2$=name2$+CHR$char%
This line adds the character whose ASCII code is char% onto the end of the string.
Understanding Colour Codes
In Section 6 we saw how to define a colour in a 256 colour mode. To remind you, the colour number consists of:- A number between 0 and 3 representing red
- A number between 0 and 3 representing green, multiplied by 4
- A number between 0 and 3 representing blue, multiplied by 16
all added together, with 128 added on if we're defining the background colour.
We could also apply a TINT number, also between 0 and 3, but multiplied by 64.
All this must have seemed very arbitrary at the time! If we examine these numbers in their binary or hexadecimal form, however, it will all make sense.
In a 256-colour mode, the colour of each dot, or pixel, on the screen is held, surprise, surprise, in one byte of the machine's memory. It would be very convenient if the number in this byte could refer directly to the amount of red, green and blue in the pixel.
To give equal space in the byte to each colour, though, would need a number of bits which is a multiple of 3 and, of course, there are eight bits in a byte. This means that we can only allocate two bits each to red, green and blue, giving us four levels of each colour - a total of 4 × 4 × 4 or 64 colours in what is supposed to be a 256-colour mode. We also have two bits left over.
Making up the Colour Number
The machine gets round this problem, as we saw, by allowing four TINT, or brightness, levels to each colour. The TINT number uses up the final two bits in each byte.It would be simple if we could define this number directly with the COLOUR or GCOL command, followed by a number between 0 and 255. Unfortunately, though, we already have the convention of using 128 and above to indicate that we're defining the background colour, which is why we have to specify the tint bits separately.
The eight bits of our colour number look like this:
fxbb ggrr
The bits representing red, green and blue are shown as r, g and b respectively.
Bit 7, shown as 'f', is the foreground/background bit. This is set to 0 if we're defining the foreground colour and 1 for the background colour. Bit 6, shown as 'x' is not used.
You should be able to see that the two 'rr' bits on their own represent a number between 0 and 3, if the other bits are set to 0.
If you move all the digits of a decimal number one place to the left and add a nought on the end, you multiply it by ten. In the same way, if you move all the bits of a binary number one place to the left, you double it. If you move them two places, you multiply it by 4, three places by 8 and so on. The two 'gg' bits, therefore, also form a number between 0 and 3, but, as it's shifted two places to the left, it's multiplied by 4, to give us 0, 4, 8 or 12.
In the same way, the two 'bb' bits make a number between 0 and 3, multiplied by 16.
The TINT number just uses the two highest, or left-hand, bits of the byte, which explains why it's a number between 0 and 3, multiplied by 64.
Experiments With Colour Numbers
You can try all this out by typing in some binary numbers. To tell the machine that the number is binary, precede it with a '%' sign in the same way that we use '&' for a hexadecimal number.You will have to try this a bit at a time if you're following this guide off the screen, as it doesn't work in a command window. First enter Mode 28 (or mode 15 if you have a standard resolution monitor). If you get an error message saying 'Bad Mode', go back to the desktop and use the Task Manager window to increase the size of the screen memory.
Now type:
COLOUR 1
You should get the Basic prompt in very dark red.
Now try:
COLOUR %10
This will produce a slightly brighter red and:
COLOUR %11
will produce a brighter red still. You have now tried all four levels of red, though with only one tint.
Now let's try the green:
COLOUR %0100
will produce a very dark green,
COLOUR %1000
will give you a brighter green and
COLOUR %1100
will give you bright green.
You can produce the corresponding shades of blue by adding two extra noughts onto these numbers.
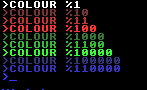
If you type:
COLOUR %1111
you will have bright red and bright green together, which will give you yellow. If you have less green than red, by typing COLOUR %0111 or COLOUR %1011, you should be able to produce two shades of orange.
The TINT number uses the top two bits of a byte, which is why it's a number between 0 and 3, multiplied by 64. Try typing:
COLOUR %101 TINT %00000000
COLOUR %101 TINT %01000000
COLOUR %101 TINT %10000000
COLOUR %101 TINT %11000000
Changing the tint number doesn't have as much effect as changing the colour number, as the different tints just fill in the gaps between the colour steps, but you should just be able to see a difference between the lines when you type them in. Remember that each line sets the colour of the following line, so the last line just sets the colour of the Basic prompt on the line below.
Now that you know how to use the bits of colour numbers, you may find it easier to define colours as binary numbers when you write your own programs. Suppose, for example, you wanted to draw a pale green circle in the middle of the screen. You would need plenty of green and just a little red and blue. Using 3 for green and 1 for each of the other two colours, then multiplying by 4 or 16 as appropriate, would give you number 45. It's a lot easier to work out, though, if you can write it as %011101. You can include it in the command:
GCOL %011101
CIRCLE FILL 600,500,100
Addresses and the Memory Map
We've referred frequently to Basic storing programs and numbers in the machine's memory and we've also mentioned memory elements. How, you may be wondering, does the machine know where in the memory anything is that it wants? The answer is that each element of the memory has a number called an address.We saw earlier how numbers move around the machine on the data bus, consisting of 32 wires or tracks on the printed circuit board. There's another set of tracks, known as the address bus. When the ARM processor wants to read in the number from a particular memory location, it puts the address number of that location on the address bus. This makes the memory chips put the number contained in the location onto the data bus, where it can be read by the processor. The same thing happens when we want to store a number in memory except that this time it's the processor that puts the number on the data bus. It also sends out a 'write' instruction on a separate wire and an address on the address bus to tell the memory chips where to store the number.
The address bus also has 32 wires, which means that it can hold over four thousand million address numbers. The way in which these numbers are used is called the memory map.
Our memory map is large enough to cope with far more memory than your machine is ever likely to contain. Most of the addresses are never used but that doesn't matter - address numbers are free! Not all the addresses that are used belong to RAM or ROM. Some are used by input/output devices, usually known as I/O. These include such things as disc controller chips, the memory controller and the chip that generates the screen display.
Each address contains one byte or eight bits. 'But this is a 32-bit machine!' you will be saying. 'Why only eight bits to an address?'
A 32-bit number actually occupies four addresses and the machine usually handles addresses four at a time. This arrangement makes it easier to deal with strings of ASCII characters, which only occupy eight bits each.
When you put a 32-bit number into memory, it is important that the address of its first byte is divisible by four. An address of this sort is said to be word-aligned.
Looking at Memory
You can take a look at what's in the memory by using a star command called *Memory. First, though, you need to know where to look. If you just try an address at random, you could well end up with an error message such as 'Abort on data transfer', which means that you tried to read from or write to an address that didn't contain any memory. Even if you were successful, you would probably find that the numbers you found were meaningless.Let's try a few experiments with memory. (If you're following the guide off the screen, you can do this in a task window.) Enter Basic and load the 'Fred2' program which we looked at earlier, so that we have something to look at, using the technique that we saw in Section 4. First make sure that your currently-selected directory is the one containing the program, then use the command:
LOAD "FRED2"
This will load the program into memory. To find out where it is, type:
PRINT ~PAGE
PAGE is the name of the address where Basic stores its programs, and the tilde (~) character tells the machine to print it in hexadecimal form.
Your machine will almost certainly tell you that PAGE is at &8F00. Basic actually uses memory from &8000. The first part of this is used for its own variables and the rest is for the program, starting at &8F00.
Try typing:
*Memory 8F00
You don't have to type the '&' symbol in star commands because the machine assumes that any numbers you include in them are hexadecimal. You should see something like this:
>PRINT ~PAGE
8F00
>*MEMORY 8F00 Address : 3 2 1 0 7 6 5 4 B A 9 8 F E D C : ASCII Data 00008F00 : 0D0A000D 203E20F4 64657246 14000D32 : ....ô > Fred2... 00008F10 : 5020F439 746E6972 20612073 656D616E : 9ô Prints a name 00008F20 : 206E6920 65776F6C 61632072 77206573 : in lower case w 00008F30 : 20687469 69206E61 6974696E 63206C61 : ith an initial c 00008F40 : 74697061 000D6C61 20EB081E 000D3231 : apital....ë 12.. 00008F50 : 20EE1B28 3AF62085 202220F1 6C207461 : (.î Y ö:ñ " at l 00008F60 : 20656E69 3A9E3B22 32000DE0 2220E820 : ine ";fi:à..2 è " 00008F70 : 74616857 20736920 72756F79 6D616E20 : What is your nam 00008F80 : 22203F65 656D616E 3C000D24 61686316 : e? "name$..<.cha 00008F90 : 973D2572 616EC028 2C24656D 0D292931 : r%=-(Àname$,1)). 00008FA0 : 63154600 25726168 6168633D 80202572 : .F.char%=char% W/ 00008FB0 : 46442620 1150000D 656D616E BD3D2432 : &DF..P.name2$=½ 00008FC0 : 72616863 5A000D25 6E20E313 20323D25 : char%..Z.ã n%=2 00008FD0 : 6EA920B8 24656D61 1964000D 72616863 : ¸ ©name$..d.char 00008FE0 : 28973D25 6D616EC1 6E2C2465 29312C25 : %=-(Áname$,n%,1) 00008FF0 : 6E000D29 61686315 633D2572 25726168 : )..n.char%=char%
Each row contains the contents of 16 addresses, each of which holds one byte. The number on the left-hand side is the address of the first of these bytes and the numbers along the top are the last figure of the address of each individual byte.
You will see that the bytes are split into groups of four, numbered backwards. The reason for this is that 32-bit numbers are stored with the lowest eight bits in the lowest address and the highest eight bits in the highest address. The location starting at &8F10, for example, shows what would have happened if we had stored &5020F439 at this address. The bottom byte, &39, is in location &8F10, the next byte, &F4, is in &8F11, &20 is in &8F12 and the highest byte, &50, is at &0F13. The next location, &0F14, is the start of the next 32-bit number.
The right-hand side of the display shows what happens when all these numbers are converted into ASCII codes. This makes it easy to pick out strings of text. A lot of this program will not make any sense - Basic doesn't store its keywords as text strings, but 'tokenises' them. Each keyword has a number between 128 and 255. The &F4 at &8F04, for example, is the token for the REM keyword in the first line. It's followed at &8F05 by &20 (a space), &3E ('>'), &20 (another space), then a string of ASCII codes making up the word 'Fred2'. Finally, in &8F0D, comes &0D, which is a Return character, which is the way all lines of Basic end. It's not important to be able to follow the program in great detail like this, but it does show how the memory works.
Byte Arrays and Indirection Operators
It is possible to write numbers into a block of memory and read them out again, but it's not a good idea to refer directly to the actual address in your program. This is because there is always a possibility that a newer version of Basic will use different address numbers and your program won't work.Look at the program called Bytes:
10 REM > Bytes 20 REM illustrates indirection operators 30 DIM block% 100 40 ?block%=&00 50 block%?1=&11 60 block%?2=&22 70 block%?3=&33 80 block%!4=&87654321 90 $(block%+8)="Hello There" 100 PRINT~block%
Notice first the DIM command in line 30. We're more used to this command followed by the name of an array with the number of elements in brackets, for example DIM array%(8). When we use the DIM command in this program, without brackets, we're telling Basic to set aside 100 bytes of memory and put the address of the first byte into variable block%. We sometimes say that block% is a pointer to this block of memory.
Jumping ahead to the last line of the program, we tell the machine to print the value of block% so that we can use it in a *Memory command later. The actual figure that you get for block% will depend on the length of your program, including spaces. This is because variables, including blocks of memory, are stored after the program listing. If you run the program provided, or type it in exactly as it's shown (but without the spaces after the line numbers), you will probably get a value of block% of &8FD4.
We transfer numbers to and from our memory block using indirection operators. There are four types of these and this program shows three of them in use.
Using Indirection Operators
The use of a question mark in line 40 means that we put number &00 into the location whose address is the value of block%, so we put a zero into address &8FD4. The expression 'block%?1' in line 50 means the same as '?(block%+1), so in this case it means 'put &11 into &8FD5. Similarly, lines 60 and 70 put &22 and &33 into &8FD6 and &8FD7 respectively.The question mark acts on a single byte. As we're using a 32-bit machine, however, we frequently need to handle four bytes, or 32 bits, at the same time. This is where our second indirection operator, an exclamation mark, comes in. Line 80 means 'put 32-bit number &87654321 into four bytes, starting at block%+4, or &8FD8'.
Our final indirection operator is a dollar sign ($) and is used for entering strings. We can't use it in the same way as ? and !, in the form block%$8, for example, so we have to enter it as $(block%+8), which means the same thing.
Line 90 means 'put the string after the equals sign into memory, its first character going into address block%+8 and finishing it with a Return character'.
We can read numbers from memory just as easily as writing them by using the indirection operators on the other side of the equals sign, for example:
x%=block%?1
You will have to start up Basic, either in a task window or from the command line and load the program into it for this exercise. When you run the program, it will print the value of block%. Use this number in a *Memory command, such as:
*Memory 8FD4+20
The number following the plus sign tells the machine to show the contents of 32 (&20) bytes. If you leave it out, you will see 256 bytes.
You will probably see something like this:
>RUN
8FD4
>*MEM.8FD4+20
Address : 7 6 5 4 B A 9 8 F E D C 3 2 1 0 : ASCII Data
00008FD4 : 33221100 87654321 6C6C6548 6854206F : .."3!Ce...Hello Th
00008FE4 : 0D657265 00000000 00000000 00000000 : ere.............
>
The first four bytes contain the single-byte numbers which were put in by the '?' indirection operators in lines 40 - 70. The 32-bit number from line 80 has gone in addresses &8FD8 to &8FDB. Notice that, because the bytes are displayed backwards, the number looks the same as it did in the listing.
The string from line 90 has gone into &8FDC onwards and ends with a Return (&0D).
The fourth type of indirection operator is '|'. This is the character obtained by pressing Shift and the backslash (\) key (just above the Return key on older machines and next to the left-hand Shift key on more modern ones). It reserves five bytes and puts a floating point number into them. Like the string indirection operator ($), you can't use an expression such as 'block%|20'. You must type |(block%+20).
Bit Shifting
If we move all the digits of a decimal number one place to the left, adding a nought on the end, we multiply it by ten. Similarly, if we move them one place to the right, we divide by ten.In the same way, moving the bits of a binary number one place to the left doubles it, moving two places multiplies it by four and so on, and moving them to the right divides it in a similar way.
We frequently need to move the bits of a number one way or the other for various reasons, not just for multiplication and division. We can move them to the left using the 'shift left' symbol '<<'. Try, for example, typing:
n%=5
PRINT n%<<1
This expression means 'n% with all its bits shifted one place to the left', so you should get the answer ten. Because n% is an integer variable, it is stored as a 32-bit number looking like this:
n%=5
0000 0000 0000 0000 0000 0000 0000 0101 =5
n%<<1
0000 0000 0000 0000 0000 0000 0000 1010 =10
n%<<2
0000 0000 0000 0000 0000 0000 0001 0100 =20
n%<<3
0000 0000 0000 0000 0000 0000 0010 1000 =40
Similarly, n%<<2 will give 20, n%<<3 40 and so on. In each case, we've shifted all 32 bits of the number one, two or three places to the left, the highest bits have disappeared off the end of the number and the lowest ones have been replaced by zeros. If you defined n% as any number and told the machine to PRINT n%<<32, the answer would be zero because you would have shifted all the bits off the end of the number and replaced them all with zeros!
Right Shifting and Signed Numbers
Shifting to the right is a little more complicated because there are two ways of doing it. We may be dealing with a signed number, that is one whose left-hand bit or most significant bit denotes whether it is positive or negative. If the number is positive, we can simply shift all the bits to the right, replacing the left-hand ones with zeros. If we tried this with negative numbers, though, we would end up with a very large positive number:n%=10
0000 0000 0000 0000 0000 0000 0000 1010 =10
n%>>>1
0000 0000 0000 0000 0000 0000 0000 0101 =5
n%=-10
1111 1111 1111 1111 1111 1111 1111 0110 =-10
n%>>>1
0111 1111 1111 1111 1111 1111 1111 1011 =2147483643
Notice that, in the above example, we used the symbol '>>>' when we moved the bits of n% to the right. This operation is known as a logical shift right and it does exactly what shift left does only in the other direction. There are times when we may want to do this when manipulating bits but, when dealing with negative signed numbers, it will produce disastrous results, as we can see.
Arithmetic and Logical Shifting
The correct way to shift a signed number to the right is to leave bit 31 (the left-most bit) as it is and also copy it into the next bit, bit 30, doing this each time we shift the bits. In this way, the bits of positive numbers are replaced by zeros and the bits of negative numbers by ones, which gives the correct result. This is known as an arithmetic shift right and has the symbol '>>':n%=-10
1111 1111 1111 1111 1111 1111 1111 0110 =-10
n%>>1
1111 1111 1111 1111 1111 1111 1111 1011 =-5
We saw in Section 8 how we could use a range of error numbers beginning with 1,073,741,824. The reason for this rather strange large number is that its hexadecimal equivalent is &40000000. In RISC OS, error numbers with bit 30 set to 1 are reserved for use within a program. This means any number between &40000000 and &7FFFFFFF, or indeed negative numbers &C0000000 to &FFFFFFFF, which should be plenty for our use!
Because &40000000 is a number in which bit 30 is a one and all the others are zeros, we can write it as 1<<30 (try typing PRINT ~1<<30). Similarly, &40000001 can be written as (1<<30)+1 and so on. This is why we used 1<<30 as an error number in Section 8.
If you managed to get through the whole of this section in one go, congratulations! Hopefully, you now have a much better understanding of your machine and the way it handles numbers.


